题目

展开代码
5. 最长回文子串
给你一个字符串 s，找到 s 中最长的回文子串。
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：
输入：s = "cbbd"
输出："bb"
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-palindromic-substring
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解答1 动态规划 转为最长子字符串（执行超时 200ms）

如果将字符串倒置，原问题变化到求最长子字符串问题：https://blog.csdn.net/x1131230123/article/details/124176271。

下图是输入"babad"的dp，需要注意取的是第一次的i行j列。

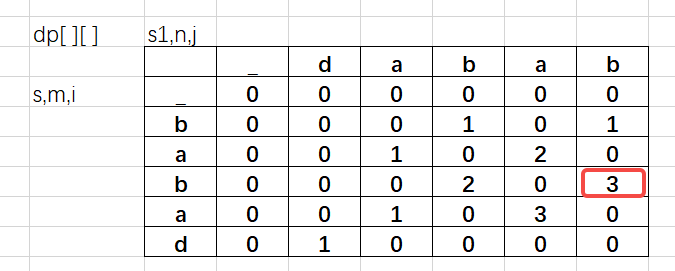
python
展开代码
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 倒序字符串，求最长公共子串
        s1 = s[::-1]
        m, n = len(s), len(s1)
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        maxlen = 0
        maxend = 0
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if s[i - 1] == s1[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = 0
                if maxlen < dp[i][j]: # 保留第一次最大的，字符串多个同长度回文只留第一次的
                    if n - j == i - dp[i][j]: # 判断回文位置，位置必须是同一个位置，比如输入acaabkaaca，回文不是acaa才行
                        maxlen = dp[i][j]
                        maxend = i
        return s[maxend - maxlen:maxend]

解答2 中心扩散 （1ms量级）

字符串非常长的时候，动态规划 $O(n^2)$ 的时间复杂度，计算量太大，而且停不下来，中心扩散法能够及时止住，时间复杂度虽然也是 $O(n^2)$ ，但期望下来小多了。

python
展开代码
class Solution:
    def expandAroundCenter(self, s, left, right):
        while left >= 0 and right < len(s) and s[left] == s[right]:
            left -= 1
            right += 1
        return left + 1, right - 1
    def longestPalindrome(self, s: str) -> str:
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = self.expandAroundCenter(s, i, i)  # 奇数个，从本字符扩散
            left2, right2 = self.expandAroundCenter(s, i, i + 1)  # 偶数个，从本字符和下一个字符扩散
            if right1 - left1 > end - start:  # 保留最大的边界
                start, end = left1, right1
            if right2 - left2 > end - start:  # 保留最大的边界
                start, end = left2, right2
        return s[start: end + 1]

解答3 动态规划 直接

这个动态规划太难想了，建议别看了==

python
展开代码
class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if n < 2:
            return s
        max_len = 1
        begin = 0
        # dp[i][j] 表示 s[i:j] 是否是回文串
        dp = [[0] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = 1
        # 递推开始
        # 先枚举子串长度
        for L in range(2, n + 1):
            # 枚举左边界，左边界的上限设置可以宽松一些
            for i in range(n):
                # 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                j = L + i - 1
                # 如果右边界越界，就可以退出当前循环
                if j >= n:
                    break
                if s[i] != s[j]:
                    dp[i][j] = 0
                else:
                    if j - i < 3:
                        dp[i][j] = 1
                    else:
                        dp[i][j] = dp[i + 1][j - 1]
                # 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if dp[i][j] and j - i + 1 > max_len:
                    max_len = j - i + 1
                    begin = i
        return s[begin:begin + max_len]