python
展开代码
#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt


def IWP_Model_Controlled(u, X, h, J1, J2, l1, l2, c1, c2, m1, m2, Kb, Kt, Ra, g):
    theta, theta_dot, phi, phi_dot = X
    A = np.array([
        [m1 * l1 ** 2 + m2 * l2 ** 2 + J1 + J2, J2],
        [J2, J2]
    ])
    B = np.array([
        [c1, 0],
        [0, (Kt * Kb / Ra) + c2]
    ])
    C = np.array([
        -(m1 * l1 + m2 * l2) * g * np.sin(theta),
        Kt * u / Ra
    ])
    acceleration = np.linalg.inv(A).dot(-B.dot(np.array([theta_dot, phi_dot])) + C)
    dXdt = np.array([theta_dot, acceleration[0], phi_dot, acceleration[1]])
    next_X = X + h * dXdt
    return next_X


class ADRC:
    def __init__(self, dt, r, h, beta1, beta2, beta3, k1, k2, b0):
        self.dt = dt
        self.r = r
        self.h = h
        self.beta1 = beta1
        self.beta2 = beta2
        self.beta3 = beta3
        self.k1 = k1
        self.k2 = k2
        self.b0 = b0
        self.v1 = 0.0
        self.v2 = 0.0
        self.z1 = 0.0
        self.z2 = 0.0
        self.z3 = 0.0
        self.u_prev = 0.0

    def fhan(self, x1, x2, r, h):
        d = r * h
        d0 = h * d
        y = x1 + h * x2
        a0 = np.sqrt(d ** 2 + 8 * r * abs(y))
        if abs(y) > d0:
            a = x2 + (a0 - d) / 2 * np.sign(y)
        else:
            a = x2 + y / h
        if abs(a) > d:
            return -r * np.sign(a)
        else:
            return -r * a / d

    def TD(self, target):
        e = self.v1 - target
        fh = self.fhan(e, self.v2, self.r, self.h)
        self.v1 += self.dt * self.v2
        self.v2 += self.dt * fh
        return self.v1, self.v2

    def ESO(self, y, u):
        e = self.z1 - y
        self.z1 += self.dt * (self.z2 - self.beta1 * e)
        self.z2 += self.dt * (self.z3 + self.b0 * u - self.beta2 * e)
        self.z3 += self.dt * (-self.beta3 * e)
        return self.z1, self.z2, self.z3

    def NLSEF(self, v1, v2, z1, z2):
        e1 = v1 - z1
        e2 = v2 - z2
        return self.k1 * e1 + self.k2 * e2

    def control(self, y, target):
        v1, v2 = self.TD(target)
        z1, z2, z3 = self.ESO(y, self.u_prev)
        u0 = self.NLSEF(v1, v2, z1, z2)
        u = (u0 - z3) / self.b0
        self.u_prev = u
        return u


def iwp_adrc_discrete():
    J1 = 0.01186
    J2 = 0.0005711
    l1 = 0.1053
    l2 = 0.14
    c1 = 0.04
    c2 = 0.0001
    m1 = 0.826
    m2 = 0.583
    Kb = 0.0987
    Kt = 0.0987
    Ra = 1.5562
    g = 9.81

    dt = 0.001
    t_total = 3
    t_steps = int(t_total / dt)

    a = m1 * l1 ** 2 + m2 * l2 ** 2 + J1 + J2
    b0 = - (Kt / (Ra * (a - J2)))
    print(b0)

    r = 30
    beta1 = 300
    beta2 = 30000
    beta3 = 1e6
    k1 = 150
    k2 = 50

    adrc = ADRC(dt, r, dt, beta1, beta2, beta3, k1, k2, b0)

    theta0 = np.deg2rad(-10)
    theta_dot0 = 0.0
    phi0 = 0.0
    phi_dot0 = 0.0
    X = np.array([theta0, theta_dot0, phi0, phi_dot0])

    theta_ref = 0.0

    theta_history = np.zeros(t_steps)
    theta_dot_history = np.zeros(t_steps)
    phi_dot_history = np.zeros(t_steps)
    time_history = np.zeros(t_steps)
    control_history = np.zeros(t_steps)

    for i in range(t_steps):
        current_time = i * dt
        current_theta = X[0]
        Vm = adrc.control(current_theta, theta_ref)
        Vm = np.clip(Vm, -50, 50)
        X = IWP_Model_Controlled(Vm, X, dt, J1, J2, l1, l2, c1, c2, m1, m2, Kb, Kt, Ra, g)

        theta_history[i] = np.rad2deg(X[0])
        theta_dot_history[i] = X[1]
        phi_dot_history[i] = X[3]
        control_history[i] = Vm
        time_history[i] = current_time

    plt.figure(figsize=(12, 5))

    plt.subplot(1, 2, 1)
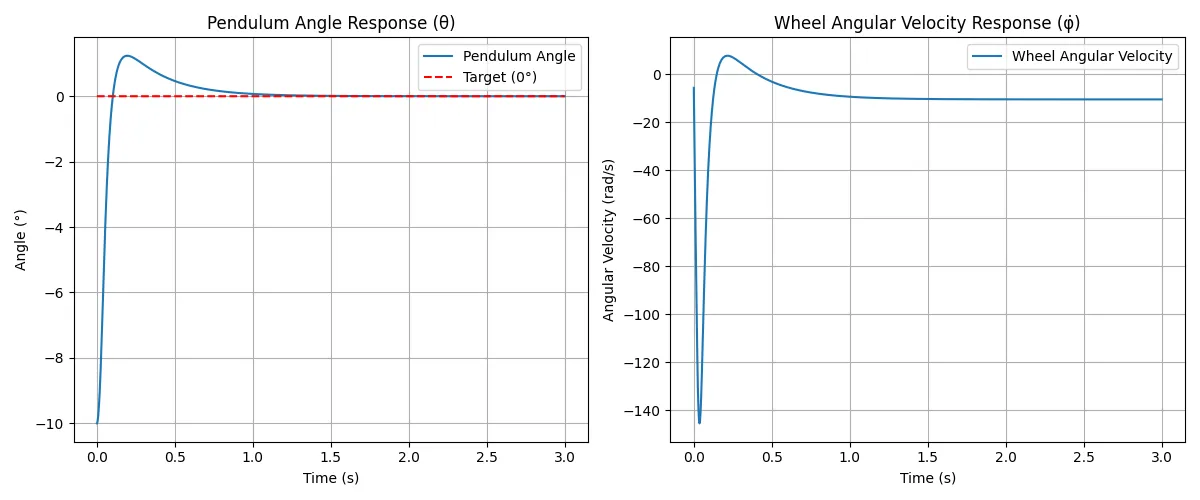
    plt.plot(time_history, theta_history, label='Pendulum Angle')
    plt.plot(time_history, np.zeros_like(time_history), 'r--', label='Target (0°)')
    plt.xlabel('Time (s)')
    plt.ylabel('Angle (°)')
    plt.title('Pendulum Angle Response (θ)')
    plt.grid(True)
    plt.legend()

    plt.subplot(1, 2, 2)
    plt.plot(time_history, phi_dot_history, label='Wheel Angular Velocity')
    plt.xlabel('Time (s)')
    plt.ylabel('Angular Velocity (rad/s)')
    plt.title('Wheel Angular Velocity Response (φ̇)')
    plt.grid(True)
    plt.legend()

    plt.tight_layout()
    plt.show()


if __name__ == '__main__':
    iwp_adrc_discrete()