推荐阅读：

为什么说快速排序是性能最好的排序算法？

6分钟演示15种排序算法

各种排序算法的使用场景

参考详细：

https://blog.csdn.net/qq_36759224/article/details/109251836

https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

https://www.cnblogs.com/onepixel/articles/7674659.html

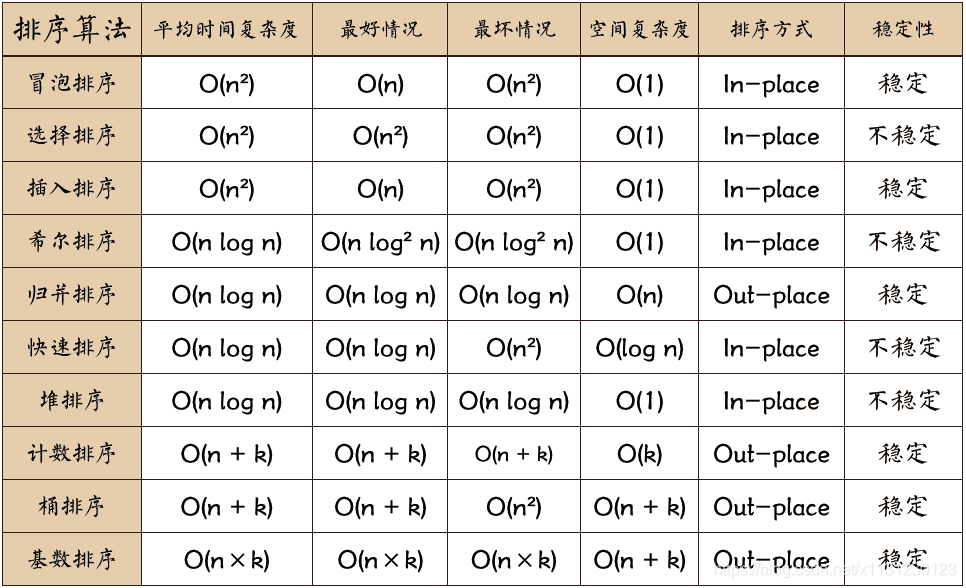
1 冒泡排序 Bubble Sort

1.1 冒泡排序 Bubble Sort

两两比较交换，直到最终。

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

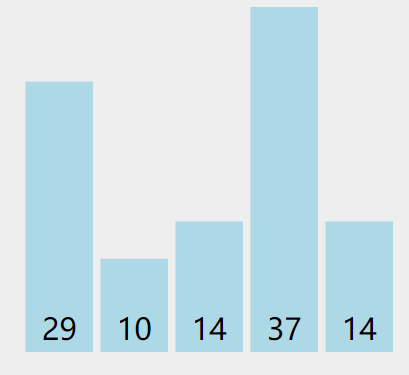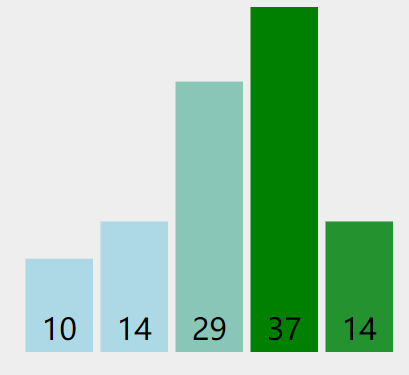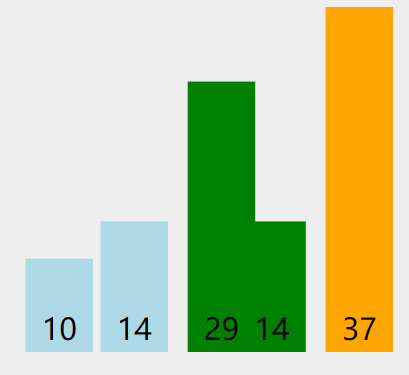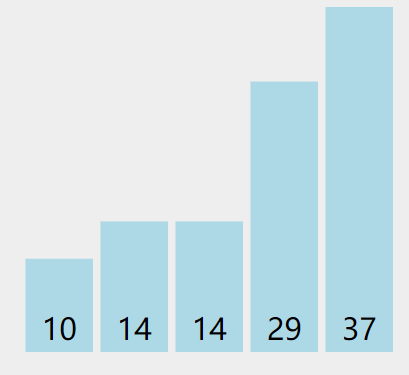
注意循环的次数。

有len(arr)个数字的话，最外面就要进行len(arr)-1次的大循环比对。

每一个大循环结束后，都有一个最大值被发现，并且放到了arr最后面。此时就不用管这个最大值，以相同方法比较剩下的数字。

python

python
展开代码
def bubbleSort(arr):
    for i in range(len(arr)-1):         # 循环len(arr)-1)次
        for j in range(len(arr)-i-1):   # 循环len(arr)-i-1次
            if arr[j] > arr[j+1]:       # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr
print(bubbleSort([3,2,5,9]))

C

c
展开代码
#include <stdlib.h>
#include <stdio.h>
void bubbleSort(int *arr, int len)
{
    int i,j;
    int temp;
    for(i=0;i< len-1;i++)
    {
        for(j=0;j< len-1-i;j++)
        {
            if(arr[j]>arr[j+1])
            {
                temp=arr[j+1];
                arr[j+1]=arr[j];
                arr[j]=temp;
            }
        }
    }
}
int main() {
    int a[]={3,5,2,1};
    bubbleSort(a,4);
    printf("%d  %d  %d  %d",a[0],a[1],a[2],a[3]);
}

1.2 添加标记的冒泡排序

当某一轮大循环中如果没有出现元素交换的情况，那么接下来的循环就没有必要进行了。元素已经全部有序了！

python

c
展开代码
def bubbleSort(arr):
    for i in range(len(arr) - 1):  # 循环len(arr)-1)次
        flag = 0
        for j in range(len(arr) - i - 1):  # 循环len(arr)-i-1次
            if arr[j] > arr[j + 1]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                flag = 1  # 有交换 变成1
        if (flag == 0):   # 还是0就说明这一轮没有交换，下一轮也就不用继续了
            print("只是循环了这么多大轮就退出了："+str(i+1))
            break
    return arr
print(bubbleSort([1, 2, 3, 2, 5, 9]))

1.3 标记有序区域的冒泡排序

在有序区域，本来就是有序的，但还是在比较，没有必要。标记出最后一次交换元素的位置避免做无所谓的比较。

python
展开代码
def bubbleSort(arr):
    lastExchangeIndex = 0
    border = len(arr) - 1  # 有序区域的边界
    for i in range(len(arr) - 1):  # 循环len(arr)-1)次
        flag = 0
        for j in range(border):  # 循环border次 交换比较出最大值
            if arr[j] > arr[j + 1]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                flag = 1  # 有交换 变成1
                lastExchangeIndex = j  # 最后一次交换元素的位置
        border = lastExchangeIndex  # 最后一次交换元素的位置
        print("最后一次交换元素的位置：" + str(border))
        if (flag == 0):  # 还是0就说明这一轮没有交换，下一轮也就不用继续了
            print("只是循环了这么多大轮就退出了：" + str(i + 1))
            break
    return arr
print(bubbleSort([3, 4, 2, 1, 5, 6, 7, 8]))

1.4 双向的鸡尾酒排序

鸡尾酒排序是为了解决一种数据分布，比如我们要对[2, 3, 4, 5, 6, 7, 1, 8]进行排序，上面冒泡法每一次去找最大值放到这一轮的后面，显得就很呆，明明直接把1放大最前面就直接完事了，直接就是有序的了。

鸡尾酒排序只需要n//2个大循环。

每个大循环中，先从左到右找到最大值放到末尾，然后从右到左找到最小值放到最前面。

新一轮的大循环在剩下的数据中进行。

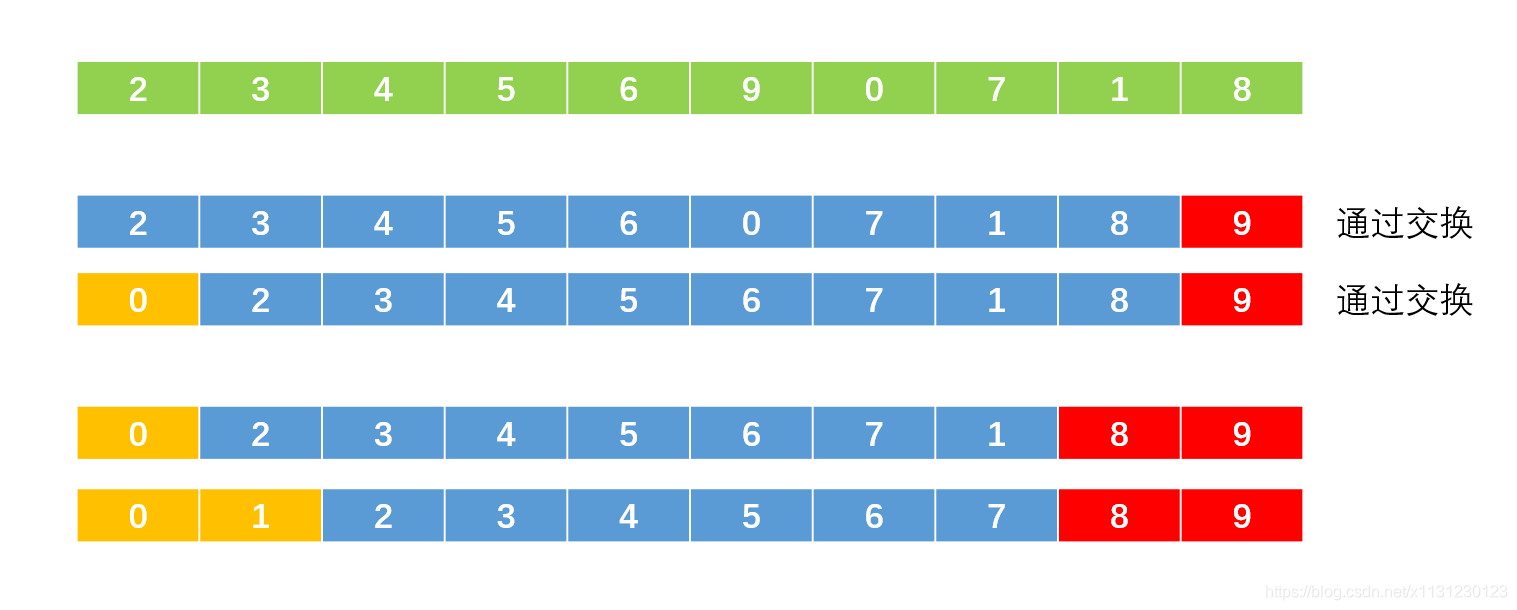
没有提前结束的代码：

python
展开代码
def bubbleSort(arr):
    for i in range(len(arr) // 2):  # 循环len(arr)-1)次
        for j in range(i, len(arr) - i - 1):  # 循环len(arr)-i-1次
            if arr[j] > arr[j + 1]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
        for j in range(len(arr) - i - 1, i, -1):  # 循环
            if arr[j - 1] > arr[j]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j - 1] = arr[j - 1], arr[j]
    return arr
print(bubbleSort([2, 3, 4, 5, 6, 9, 2, 7, 1, 8]))

带提前结束的逻辑：

python
展开代码
def bubbleSort(arr):
    for i in range((int)(len(arr) / 2)):  # 循环len(arr)-1)次
        flag1 = 0
        for j in range(i,len(arr) - i - 1):  # 循环len(arr)-i-1次
            if arr[j] > arr[j + 1]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                flag1 = 1  # 有交换 变成1
        flag2 = 0
        for j in range(len(arr) - i - 1, i, -1):  # 循环
            if arr[j - 1] > arr[j]:  # 如果这个数大于后面的数就交换两者的位置
                arr[j], arr[j - 1] = arr[j - 1], arr[j]
                flag2 = 1  # 有交换 变成1
        if (flag1 == 0  and flag2==0):  # 都没交换过 提前结束大循环
            break
    return arr
print(bubbleSort([2, 3, 4, 5, 6, 9, 0, 7, 1, 8]))

2 选择排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

第1轮：第1个元素和其余的元素比较，记录最小元素的下标。交换。

第2轮：第2个元素和其余的元素比较，记录最小元素的下标。交换。

[2, 3, 4, 5, 6, 9, 0, 7, 1, 8] 原始数据

[0, 3, 4, 5, 6, 9, 2, 7, 1, 8] 第1轮结束后

[0, 1, 4, 5, 6, 9, 2, 7, 3, 8] 第2轮结束后

[0, 1, 2, 5, 6, 9, 4, 7, 3, 8]

[0, 1, 2, 3, 6, 9, 4, 7, 5, 8]

[0, 1, 2, 3, 4, 9, 6, 7, 5, 8]

[0, 1, 2, 3, 4, 5, 6, 7, 9, 8]

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] OK

……

python
展开代码
def selection_sort(arr):  # 长度 5: 0 1 2 3 4
    for i in range(len(arr) - 1):  # 0 1 2 3
        min_index = i  # 记录最小数的下标 0 1 2 3
        for j in range(i + 1, len(arr)):  # 1 2 3 4
            if arr[j] < arr[min_index]:  # 1234 < 0 ?
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]  # 交换
    return arr
print(selection_sort([2, 3, 4, 5, 6, 9, 0, 7, 1, 8]))

3 插入排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

和整理扑克牌相似，假设前面的都已经有序，选择当前牌去插入到这个有序序列。

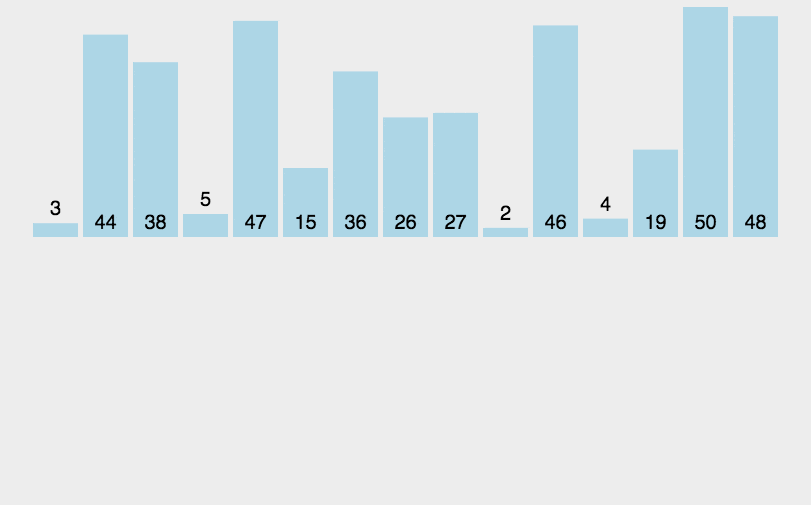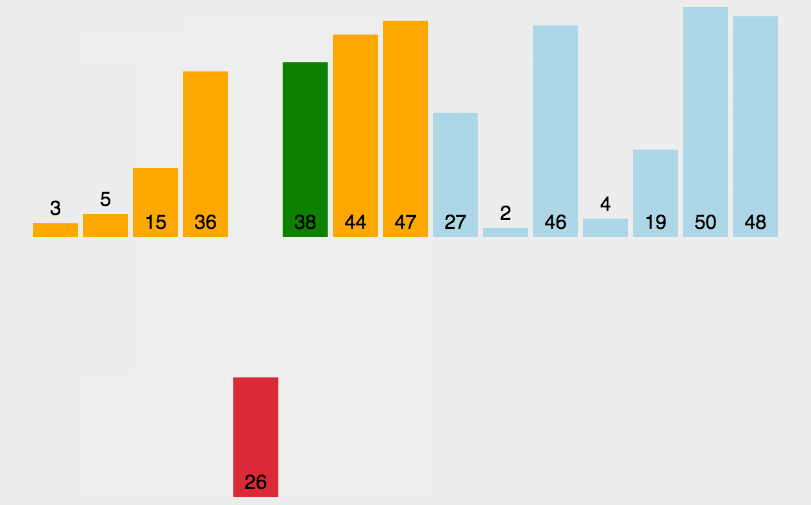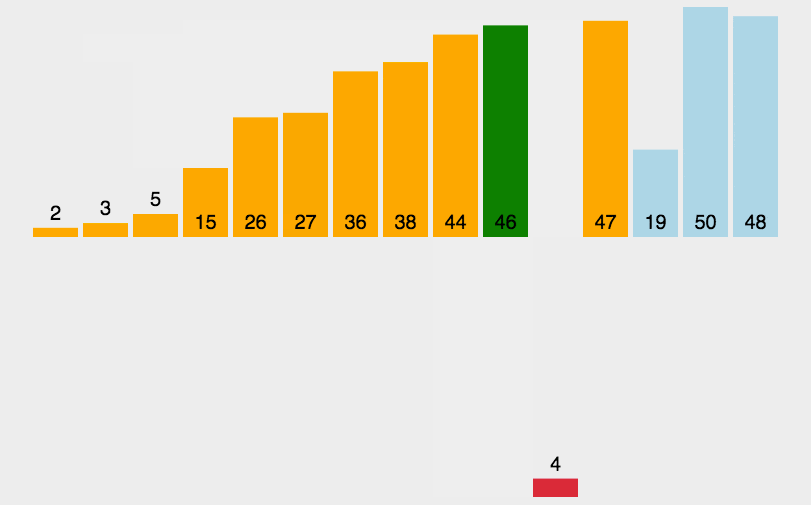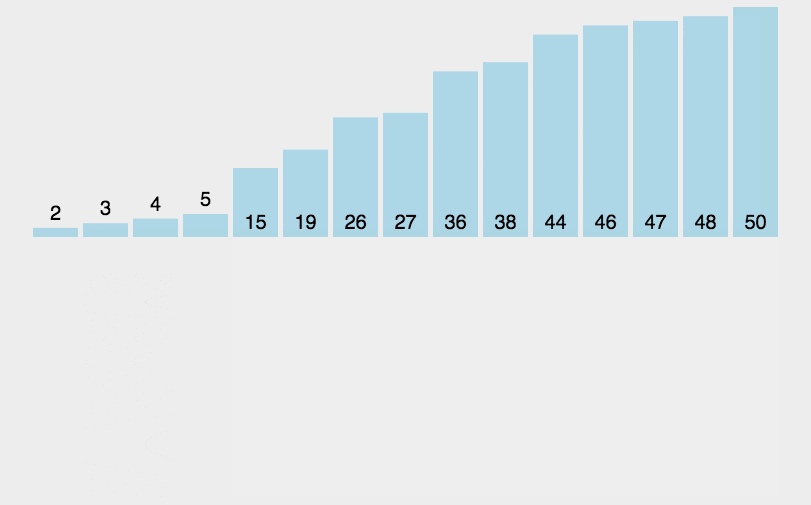
假面的都是有序的。把新元素插入进去。

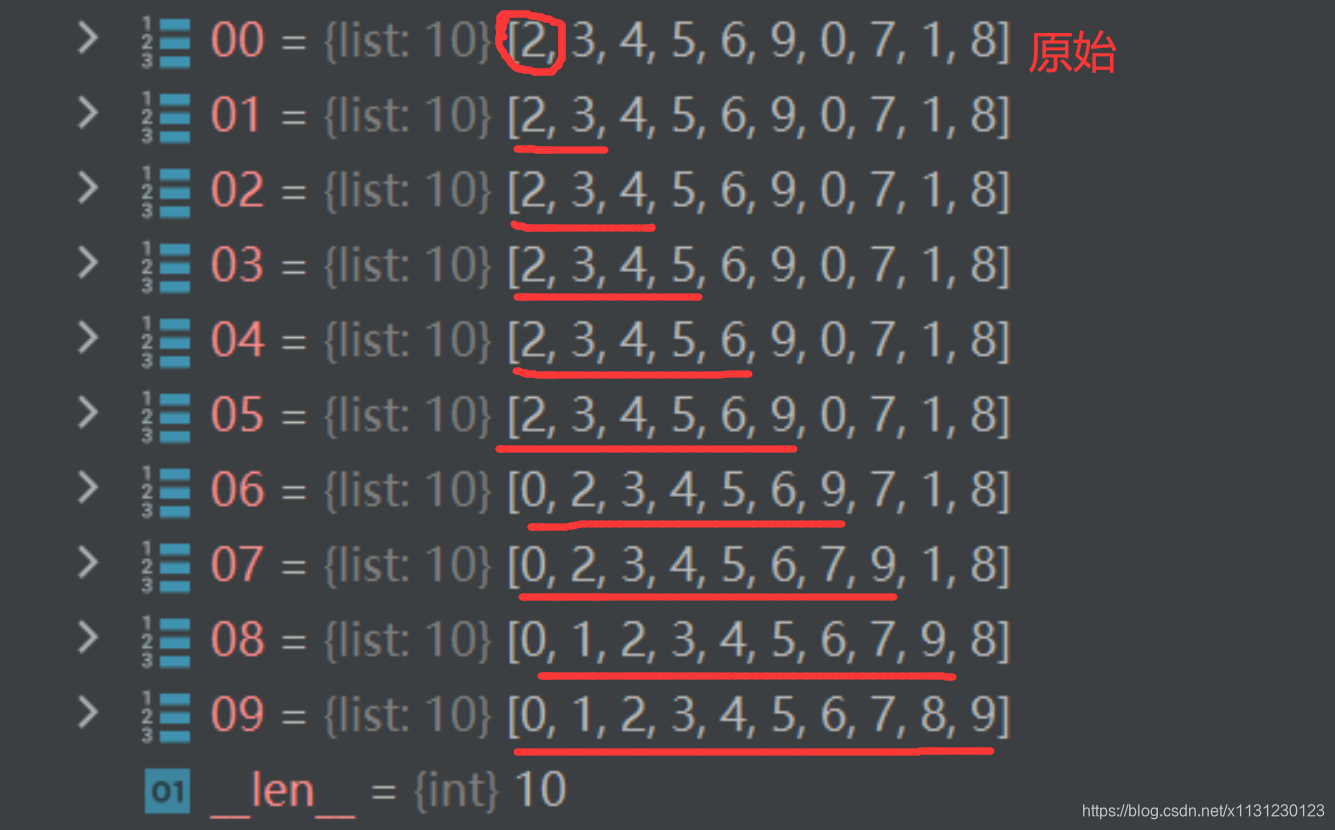
python
展开代码
def insertion_sort(arr): # 5: 0 1 2 3 4
    for i in range(1, len(arr)):    # 1 2 3 4
        tmp = arr[i]                # 1 2 3 4 从前到后遍历
        j = i-1                     # 0 1 2 3 从前到后遍历
        while j >= 0 and arr[j] > tmp:  # j从后向前  每次比较j是否大于取到的元素
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = tmp
    return arr
print(insertion_sort([2, 3, 4, 5, 6, 9, 0, 7, 1, 8]))

4 希尔排序

在这个博客https://www.cnblogs.com/chengxiao/p/6104371.html有下面这幅图：

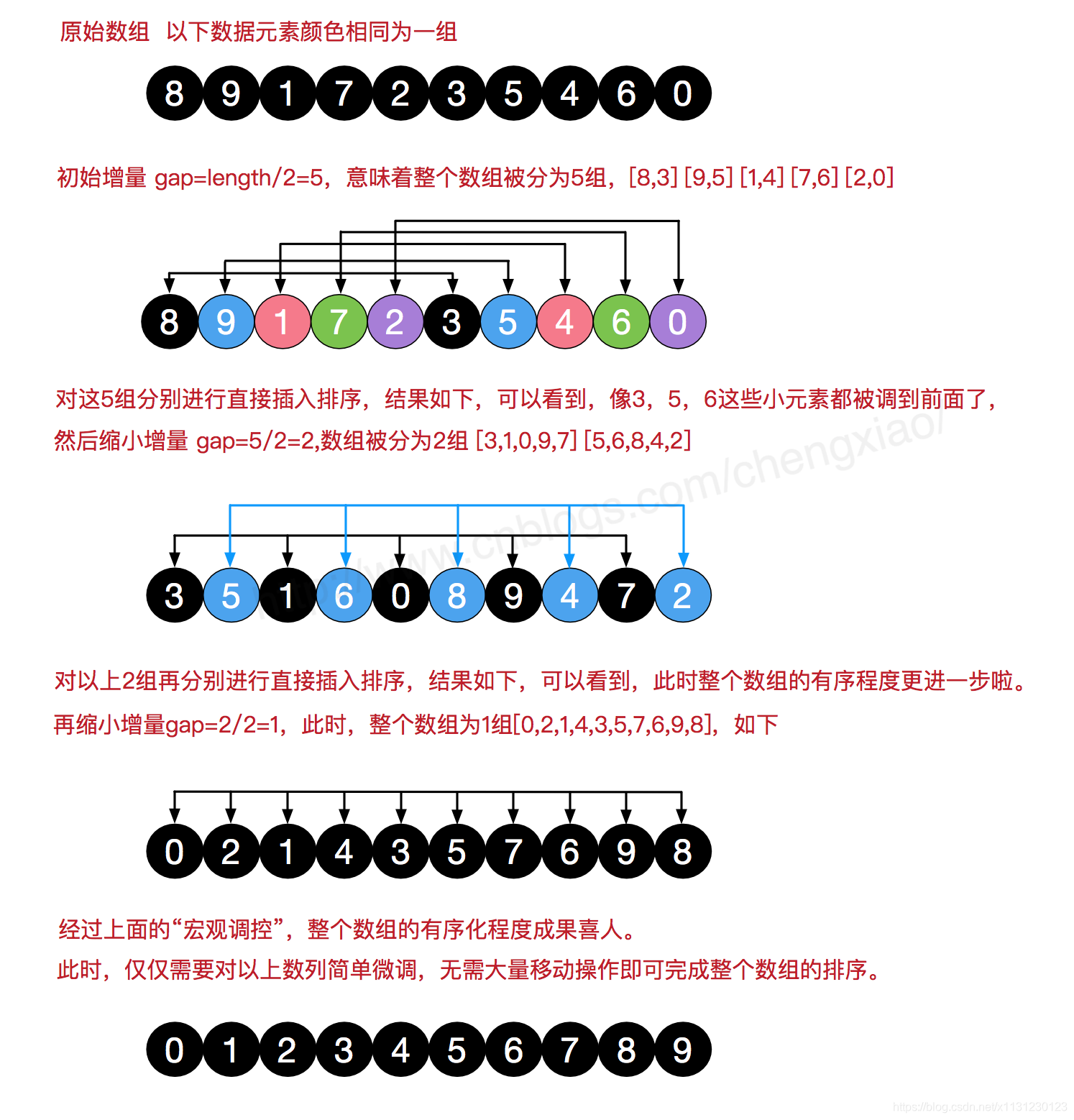
这算法真是感人涕下，算法过程有点曲折。我觉得关注点放在“宏观调控”数据分布上就好。

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

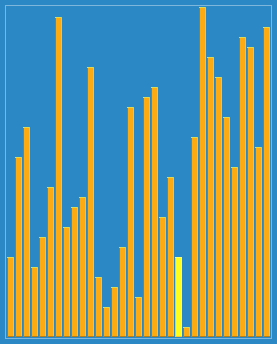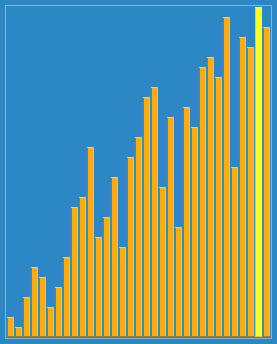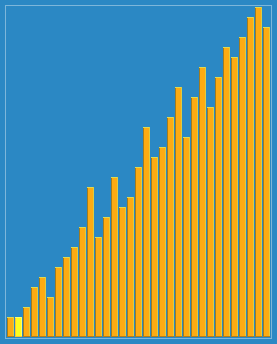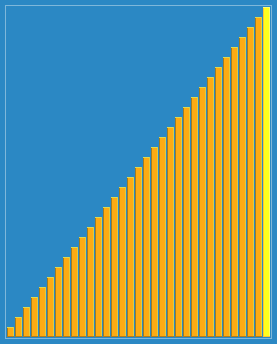
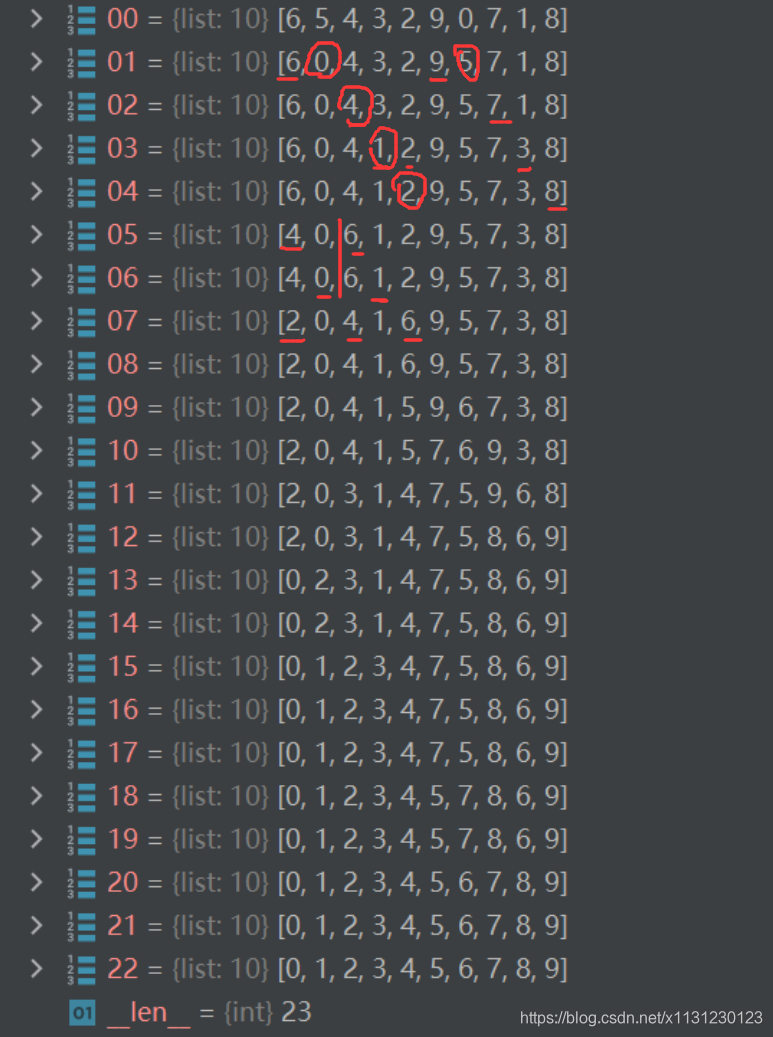
大循环下：

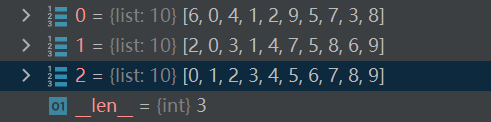
python
展开代码
def shell_sort(arr):  # 长度8
    d = len(arr) // 2  # d=4
    while d >= 1:
        for i in range(d, len(arr)):  # 4~7 2~7 1~7
            tmp = arr[i]  # 4~7 2~7 1~7
            j = i - d  # 0~3 0~5 0~6
            while j >= 0 and tmp < arr[j]:  # 后面的牌<前面的牌
                arr[j + d] = arr[j]  # 大牌往后放
                j -= d
            arr[j + d] = tmp
            print("da")
            print(j + d, j + 2 * d, arr)
        print("----")  # 每一轮排序后打印一次
        d //= 2  # d=2 d=1  d=0退出
    return arr
print(shell_sort([6, 5, 4, 3, 2, 9, 0, 7, 1, 8]))

5 归并排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

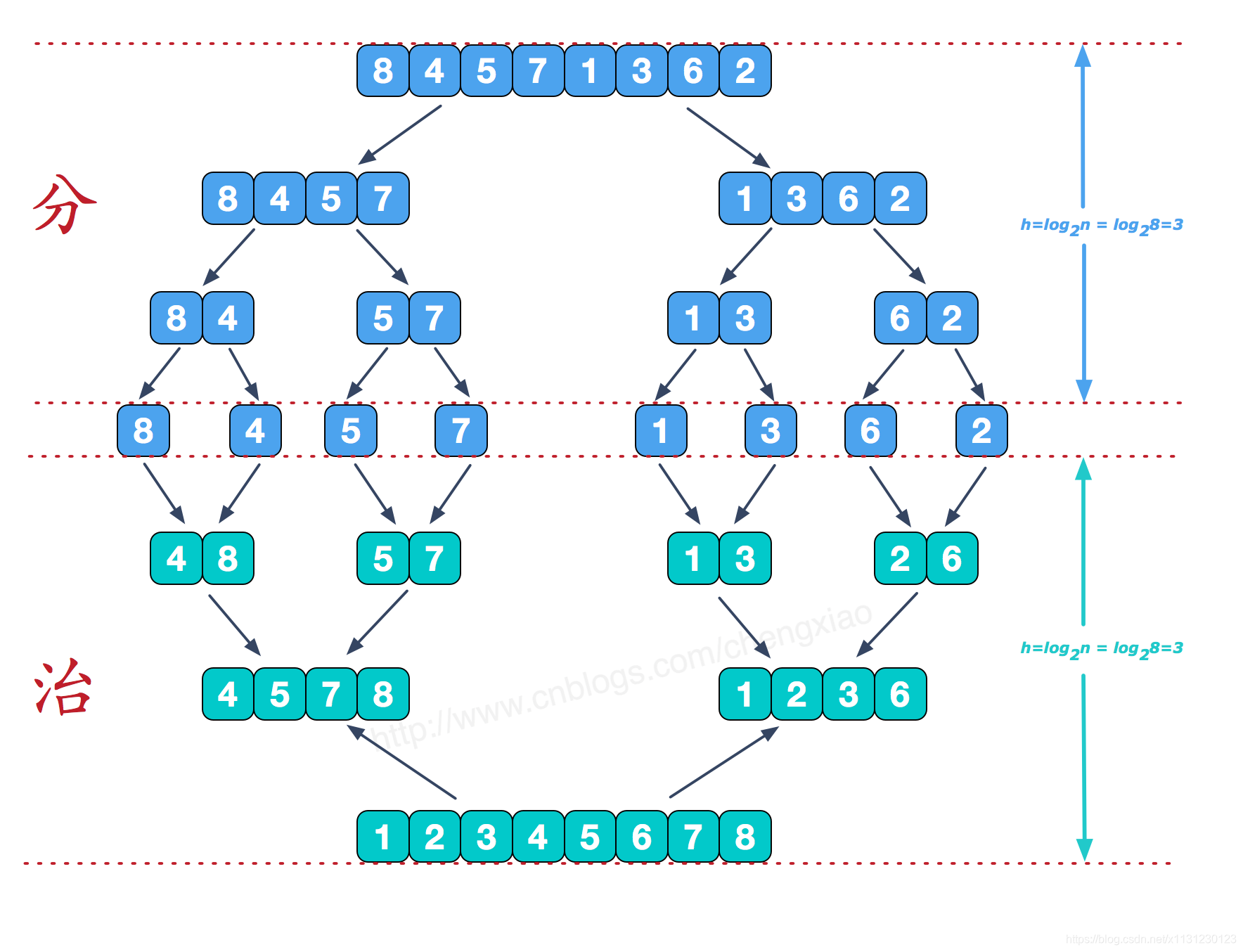
python
展开代码
def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0))
    while right:
        result.append(right.pop(0))
    return result
def mergeSort(arr):
    if(len(arr)<2):
        return arr
    middle = len(arr)//2   # 中间
    left, right = arr[0:middle], arr[middle:]  # 分离
    return merge(mergeSort(left), mergeSort(right))  # 递归
print(mergeSort([ 4,5,1,2,3,2,1,2,7,6]))

加断点，分离后看看分离成啥样子了。

返回合并前看看合并的情况。

[ 4,5,1,2,3,2,1,2,7,6]

[4, 5, 1, 2, 3][2, 1, 2, 7, 6]

[4, 5][1, 2, 3]

[4][5]

[4, 5]合并了

[1][2, 3]

[2][3]

[2, 3]合并了

[1, 2, 3]合并了

[1, 2, 3, 4, 5]合并了

[2, 1][2, 7, 6]

[2][1]

[1, 2]合并了

[2][7, 6]

[7][6]

[6, 7]合并了

[2, 6, 7]合并了

[1, 2, 2, 6, 7]合并了

[1, 1, 2, 2, 2, 3, 4, 5, 6, 7]合并了

6 快速排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

很重要的一个算法，考研必备。想理解这个算法，必须追溯运行过程。

每一个递归过程其实就是在找一个合适的坑，这个坑基准填下去后，能够让 基准前面的数都是小于等于的 基准后面的都是大于等于的。

在一个递归过程，经过巧妙玩坑填坑。

递归过程：

（1）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=0 right=9 )

[ x,5,1,2,3,2,1,2,7,6] 挖掉基准作为一个坑，从右到左找小于基准的往前面填 x代表一个坑

[ 2,5,1,2,3,2,1,x,7,6] 从左到右找大于基准的往后面坑里填

[ 2,x,1,2,3,2,1,5,7,6]

[ 2,1,1,2,3,2,x,5,7,6]

[ 2,1,1,2,3,2,4,5,7,6] 此时left=right=6 填到最后 找到了合适的坑

（2）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=0 right=5 )

[ x,1,1,2,3,2,4,5,7,6]

[ 1,1,x,2,3,2,4,5,7,6]

[ 1,1,2,2,3,2,4,5,7,6] left=right=2

（3）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=0 right=1 )

[ x,1,2,2,3,2,4,5,7,6]

[ 1,1,2,2,3,2,4,5,7,6] left=right=0

（4）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=3 right=5 )

[ 1,1,2,x,3,2,4,5,7,6]

[ 1,1,2,2,3,2,4,5,7,6] left=right=3

（5）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=4 right=5 )

[ 1,1,2,2,x,2,4,5,7,6]

[ 1,1,2,2,2,3,4,5,7,6] left=right=3

（6）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=7 right=9 )

[ 1,1,2,2,2,3,4,x,7,6]

[ 1,1,2,2,2,3,4,5,7,6] left=right=7

（7）执行 partition( [ 4,5,1,2,3,2,1,2,7,6] left=8 right=9 )

[ 1,1,2,2,2,3,4,5,x,6]

[ 1,1,2,2,2,3,4,5,6,7] left=right=9

python
展开代码
def partition(arr, left, right):
    # 归位操作，left，right 分别为数组左边和右边的位置索引
    tmp = arr[left]
    while left < right:
        while left < right and arr[right] >= tmp:  # 从右边找比 tmp 小的数，如果比 tmp 大，则移动指针
            right -= 1                             # 将指针左移一个位置
        arr[left] = arr[right]                     # 将右边的值写到左边的空位上
        while left < right and arr[left] <= tmp:   # 从左边找比 tmp 大的数，如果比 tmp 小，则移动指针
            left += 1                              # 将指针右移一个位置
        arr[right] = arr[left]                     # 将左边的值写到右边的空位上
    arr[left] = tmp                                # 把 tmp 归位
    return left                   # 返回 left，right 都可以，目的是便于后面的递归操作对左右两部分进行排序
def quick_sort(arr, left, right):          # 快速排序
    if left < right:
        mid = partition(arr, left, right)
        quick_sort(arr, left, mid-1)       # 对左半部分进行归位操作
        quick_sort(arr, mid+1, right)      # 对右半部分进行归位操作
    return arr
print(quick_sort([ 4,5,1,2,3,2,1,2,7,6],0,9))

7 堆排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

堆是一种数据结构，也叫优先级队列，有大顶堆、小顶堆。

这里有一个堆的介绍：https://blog.csdn.net/x1131230123/article/details/104493844

python里有一个实现好的了heapq（堆队列、优先级队列）API。

所以堆排序：

用heappush方法将iterable中的元素一个一个压入堆（插入列表末尾，然后上滤），这是一个构建堆的过程。然后利用heappop方法一直取出堆顶元素（下滤到列表末尾，然后删除）。

python
展开代码
import heapq
def heapsort(iterable):
    h = []
    for value in iterable:
        heapq.heappush(h, value)
    return [heapq.heappop(h) for i in range(len(h))]
print(heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]))

构建堆还可以使用别的方法，Floyd 建堆算法（自下而上的下滤），就地运算：

python
展开代码
import heapq
def heapsort(iterable):
    heapq.heapify(iterable) #Floyd 建堆算法（自下而上的下滤）
    return [heapq.heappop(iterable) for i in range(len(iterable))]
print(heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]))

或者自行写一个（依据自下而上的下滤）：

python
展开代码
def buildMaxHeap(arr):
    for i in range(len(arr) // 2 - 1, -1, -1):  # len(arr)//2-1 是最后一个有孩子的节点。从这个节点开始，自下而上找所有有孩子的父节点。
        heapify(arr, i)  # 下滤这个i节点
# 下滤这个i节点
def heapify(arr, i):
    left = 2 * i + 1  # 左孩子
    right = 2 * i + 2  # 右孩子
    largest = i  # 父亲节点i
    if left < arrLen and arr[left] > arr[largest]: # 左孩子index<列表总长度（没有左孩子就会不满足这个条件） and 左孩子数值>其父亲节点数值
        largest = left   # largest=左孩子index
    if right < arrLen and arr[right] > arr[largest]: # 右孩子index<列表总长度（没有右孩子就会不满足这个条件）  and  右孩子数值>其父亲节点数值或者左孩子数值
        largest = right  # largest=右孩子index
    if largest != i:   # 父亲节点i并不是最大的  左孩子或者右孩子是最大的  index放在largest里面
        swap(arr, i, largest)  # arr里交换数值 把左孩子或者右孩子中最大的和父亲节点数值交换    此时largest这个index指向了之前左孩子或者右孩子的index 并不是最大的了
        heapify(arr, largest)  # 为了维持堆的特性 自下而上 下滤小元素，在前一操作中，较大孩子数值和父亲数值交换了，交换后，父亲数值可能与新孩子数值冲突，所以继续下滤操作
def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def heapSort(arr):
    global arrLen
    arrLen = len(arr)
    buildMaxHeap(arr)  # 堆化  建立堆   大顶堆
    for i in range(len(arr) - 1, 0, -1): # len(arr)-1是最末尾元素  1是根节点的左孩子
        swap(arr, 0, i)  #将根节点数值和最末尾元素交换
        arrLen -= 1      #堆长度减去1
        heapify(arr, 0)  # 下滤 这个新的根节点，但此时堆的size已经减1 也就是说不管列表最后一个元素了，是最大值或者说是有序的一些数值
    return arr
# 下滤 是父亲节点和孩子不断比较
# 上滤 是孩子节点和父亲不断比较
print(heapSort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]))

8 计数排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

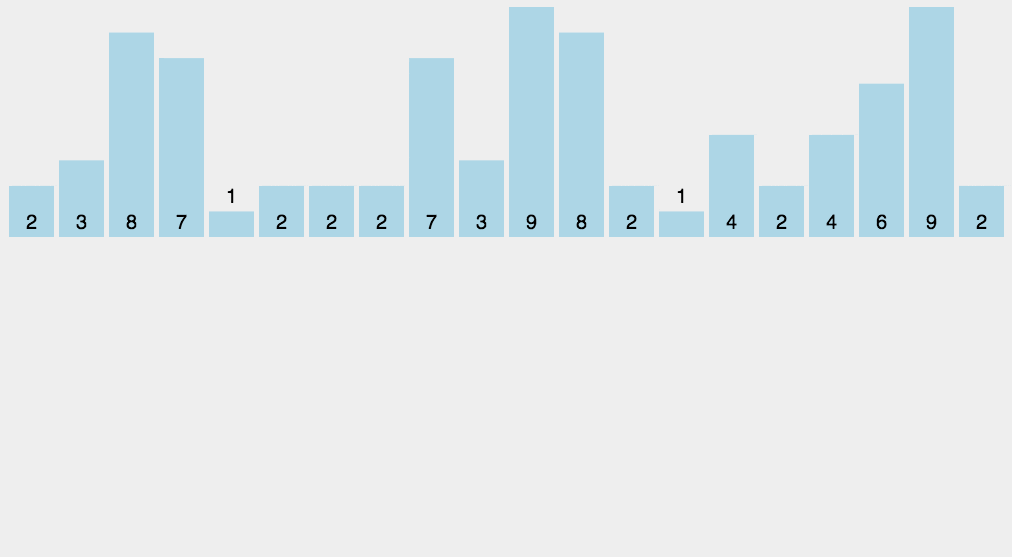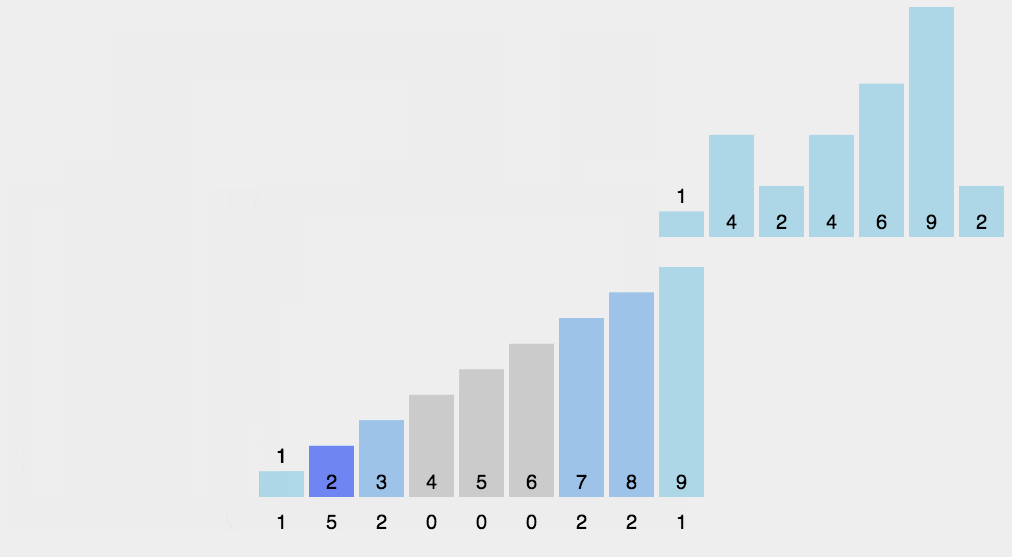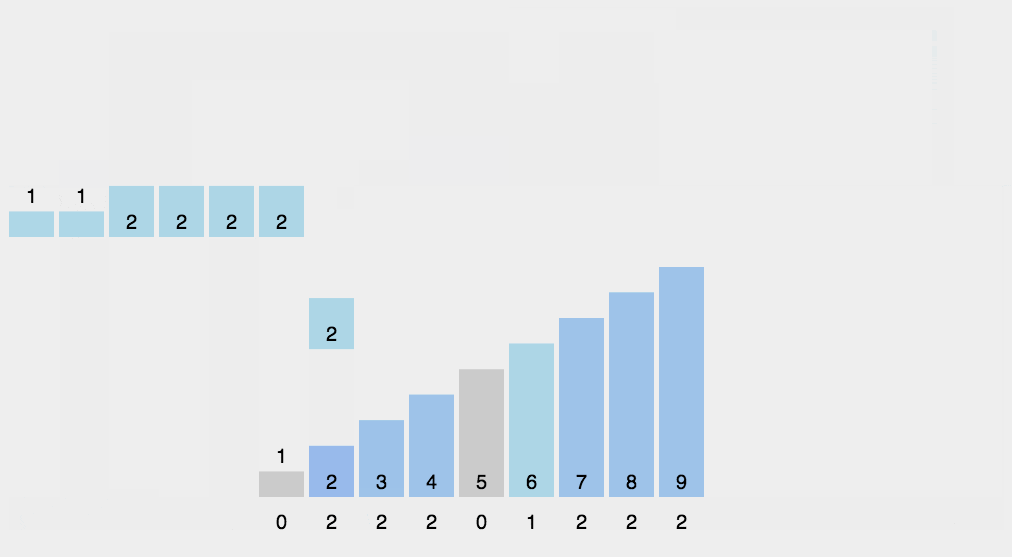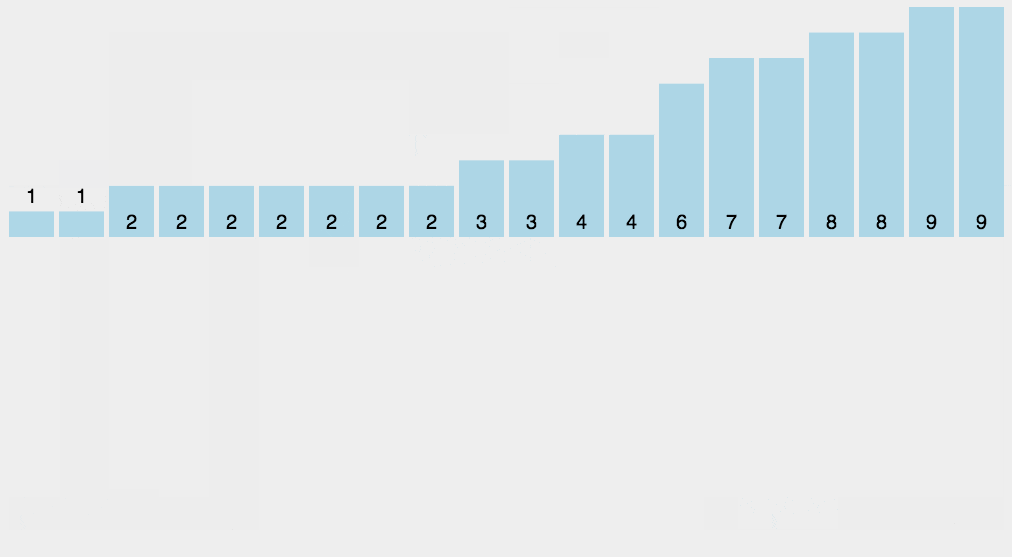
python
展开代码
def countingSort(arr, maxValue):
    bucketLen = maxValue+1
    bucket = [0]*bucketLen  # 生成一个bucketLen长度的列表bucket
    sortedIndex =0
    arrLen = len(arr)  # 待排序的列表元素个数
    for i in range(arrLen):  # 遍历待排序的列表的每一个元素
        # if not bucket[arr[i]]:  # bucket中对应位置此时是0
        #     bucket[arr[i]]=0    # 把这个位置给0 这2句多余的 本来初始时刻列表bucket里全是0 代表有0个元素
        bucket[arr[i]]+=1  # 把这个元素对应位置加1  表示统计到了待排序的列表又多了一个这个数值
    for j in range(bucketLen):  # 从0遍历bucketLen
        while bucket[j]>0:
            arr[sortedIndex] = j  # 按顺序装填到 arr
            sortedIndex+=1
            bucket[j]-=1
    return arr
print(countingSort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0],9))

计数排序思想很简单，用空间换时间，比较适合方差不大的一堆数据，但如果待排序的列表是这样：

[1000000,2,1,3]

这初始化bucket空间的时候，申请size为1000001个的列表，可见很多空间被浪费了，这时候就该桶排序上场更好。

同时，计数排序也不能用于浮点数的排序。

9 桶排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

创建桶，每个桶装一定范围区间内的数据。

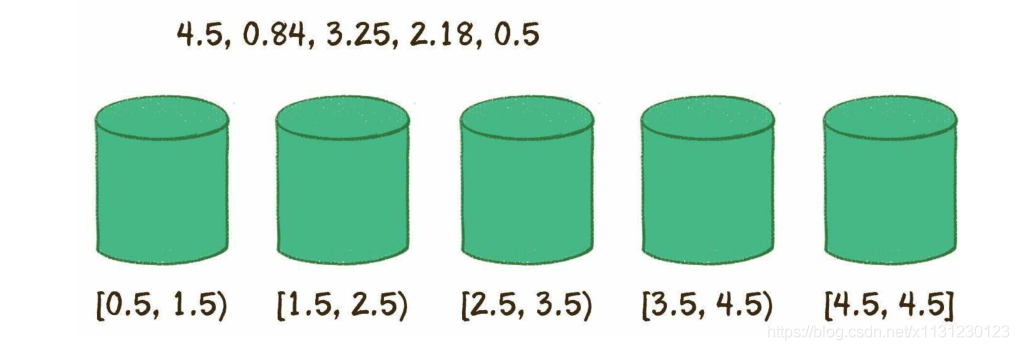
对每个桶内的数据分别排序。

最后依次输出每个桶的数据。

什么时候最快

当输入的数据可以均匀的分配到每一个桶中。

什么时候最慢

当输入的数据被分配到了同一个桶中。

c
展开代码
def count_sort(arr):
    if len(arr) < 2:  # 如果数组长度小于 2 则直接返回
        return arr
    # 1 遍历得到最大值 最小值 差值
    maxv = max(arr)
    minv = min(arr)
    d = maxv - minv
    # 2 初始化桶
    bucketnum = 5  # 想要五个桶
    bucketlist = [[] for _ in range(bucketnum)]
    print(bucketlist)
    # 3 遍历原始队列
    for i in range(0, len(arr)):
        bucketlist[(int)((arr[i] - minv) * (bucketnum - 1) / d)].append(arr[i])
    print(bucketlist)
    # 4 每个桶内部排序，可以用一些别的排序算法
    for i in range(bucketnum):
        bucketlist[i].sort()
    print(bucketlist)
    # 5 输出每个桶
    sortarr=[]
    for i in range(bucketnum):
        sortarr.extend(bucketlist[i])
    print(sortarr)
    return sortarr
print(count_sort([1.2, 3, 5, 7, 9.4, 2.2, 4, 6.6, 8, -1.5]))

10 基数排序

平均时间复杂度，最好时间复杂度，最差时间复杂度，空间复杂度，稳定否

arr=[13123,343,554,821,6654,644]

第一次循环结束后，arr根据个位数字全部写入了buckets：[[], [821], [], [13123, 343], [554, 6654, 644], [], [], [], [], []]

然后flatten桶后，赋值给arr,此时arr=[821, 13123, 343, 554, 6654, 644]。

第2次循环结束后，

buckets=[[], [], [821, 13123], [], [343, 644], [554, 6654], [], [], [], []]

arr=[821, 13123, 343, 644, 554, 6654]

第3次循环结束后，

buckets=[[], [13123], [], [343], [], [554], [644, 6654], [], [821], []]

arr=[13123, 343, 554, 644, 6654, 821]

第4次循环结束后，

buckets=[[343, 554, 644, 821], [], [], [13123], [], [], [6654], [], [], []]

arr=[343, 554, 644, 821, 13123, 6654]

第5次循环结束后，

buckets=[[343, 554, 644, 821, 6654], [13123], [], [], [], [], [], [], [], []]

arr=[343, 554, 644, 821, 6654, 13123]

python
展开代码
def radix_sort(arr):
    max_num = max(arr)
    it = 0
    while 10 ** it <= max_num:
        buckets = [[] for _ in range(10)]
        for var in arr:
            digit = (var // 10 ** it) % 10   # 依次取一位数
            buckets[digit].append(var)
        # 分桶完成
        arr.clear()
        for buc in buckets:
            arr.extend(buc)
        it += 1
    return arr
print(radix_sort([13123,343,554,821,6654,644]))