判断线段是否相交的办法（使用了向量叉积的方法）：

c
展开代码
首先，通过给定的线段端点坐标p1、p2、p3和p4构建了四个向量v1、v2、v3和v4：
v1表示从p1指向p2的向量，其分量为[p2[0] - p1[0], p2[1] - p1[1]]。
v2表示从p3指向p4的向量，其分量为[p4[0] - p3[0], p4[1] - p3[1]]。
v3表示从p1指向p3的向量，其分量为[p3[0] - p1[0], p3[1] - p1[1]]。
v4表示从p1指向p4的向量，其分量为[p4[0] - p1[0], p4[1] - p1[1]]。
接下来，计算了两个叉积cross1和cross2：
cross1表示v1和v3的叉积，计算公式为v1[0] * v3[1] - v1[1] * v3[0]。
cross2表示v1和v4的叉积，计算公式为v1[0] * v4[1] - v1[1] * v4[0]。
最后，根据两个叉积的乘积进行判断：
如果cross1和cross2的乘积小于等于0，意味着v1和v3位于不同的半平面或者其中一个线段的某个端点在另一个线段上，这时可以判断两条线段相交。
如果cross1和cross2的乘积大于0，意味着v1和v3位于同一侧或者两个线段没有交点，这时可以判断两条线段不相交。
根据以上逻辑，如果条件满足，则返回True表示线段相交，否则返回False表示线段不相交。

Python代码实现：

python
展开代码
class point():  # 定义类
    def __init__(self, x, y):
        self.x = x
        self.y = y
def cross(p1, p2, p3):  # 跨立实验
    x1 = p2.x - p1.x
    y1 = p2.y - p1.y
    x2 = p3.x - p1.x
    y2 = p3.y - p1.y
    return x1 * y2 - x2 * y1
def has_intersect(p1, p2, p3, p4):  # 判断两线段是否相交
    # 快速排斥，以l1、l2为对角线的矩形必相交，否则两线段不相交
    if (max(p1.x, p2.x) >= min(p3.x, p4.x)  # 矩形1最右端大于矩形2最左端
            and max(p3.x, p4.x) >= min(p1.x, p2.x)  # 矩形2最右端大于矩形最左端
            and max(p1.y, p2.y) >= min(p3.y, p4.y)  # 矩形1最高端大于矩形最低端
            and max(p3.y, p4.y) >= min(p1.y, p2.y)):  # 矩形2最高端大于矩形最低端
        # 若通过快速排斥则进行跨立实验
        if (cross(p1, p2, p3) * cross(p1, p2, p4) <= 0
                and cross(p3, p4, p1) * cross(p3, p4, p2) <= 0):
            D = True
        else:
            D = False
    else:
        D = False
    return D
def are_lines_intersect(p1, p2, p3, p4):
    p1 = point(p1[0], p1[1])
    p2 = point(p2[0], p2[1])
    p3 = point(p3[0], p3[1])
    p4 = point(p4[0], p4[1])
    if has_intersect(p1, p2, p3, p4):
        return True
    else:
        return False
def compute_intersection(p1, p2, p3, p4):
    if p1[0] == p2[0]:  # p1p2为垂直线
        x = p1[0]
        slope2 = (p4[1] - p3[1]) / (p4[0] - p3[0])
        intercept2 = p3[1] - slope2 * p3[0]
        y = slope2 * x + intercept2
    elif p3[0] == p4[0]:  # p3p4为垂直线
        x = p3[0]
        slope1 = (p2[1] - p1[1]) / (p2[0] - p1[0])
        intercept1 = p1[1] - slope1 * p1[0]
        y = slope1 * x + intercept1
    else:
        slope1 = (p2[1] - p1[1]) / (p2[0] - p1[0])
        slope2 = (p4[1] - p3[1]) / (p4[0] - p3[0])
        intercept1 = p1[1] - slope1 * p1[0]
        intercept2 = p3[1] - slope2 * p3[0]
        if slope1 == slope2:
            # 斜率相等的时候，如果线段重合，交点是无数个，这里返回断点表达此意
            if p1[0] <= p3[0] <= p2[0]:
                return p3
            if p1[0] <= p4[0] <= p2[0]:
                return p4
        else:
            x = (intercept2 - intercept1) / (slope1 - slope2)
            y = slope1 * x + intercept1
    return [x, y]
if __name__ == '__main__':
    p1 = [0, 5]
    p2 = [10, 5]
    p3 = [0, 10]
    p4 = [10, 10]
    # p1 p2 是一条线段
    # p3 p4 是另一条线段
    # 判断是否相交，相交且求交点
    if are_lines_intersect(p1, p2, p3, p4):
        print(compute_intersection(p1, p2, p3, p4))
        x, y = compute_intersection(p1, p2, p3, p4)
    else:
        print("No intersection")
    # 画图
    import matplotlib.pyplot as plt
    # 样式是波浪线
    plt.plot([p1[0], p2[0]], [p1[1], p2[1]], color='r')
    # 样式是点线
    plt.plot([p3[0], p4[0]], [p3[1], p4[1]], color='b', linewidth=4, linestyle=':')
    # 加注释
    plt.annotate('p1', xy=(p1[0], p1[1]), xytext=(p1[0] + 10, p1[1] + 10))
    plt.annotate('p2', xy=(p2[0], p2[1]), xytext=(p2[0] + 10, p2[1] + 10))
    plt.annotate('p3', xy=(p3[0], p3[1]), xytext=(p3[0] + 10, p3[1] + 10))
    plt.annotate('p4', xy=(p4[0], p4[1]), xytext=(p4[0] + 10, p4[1] + 10))
    try:
        # 绘制交点
        plt.scatter(x, y, color='g', marker='o')
        # 给交点加注释
        plt.annotate('intersection', xy=(x, y), xytext=(x, y),
                     arrowprops=dict(facecolor='g', shrink=0.05))
    except:
        pass
    # 坐标轴等距
    plt.axis('equal')
    plt.show()

绘制的图：

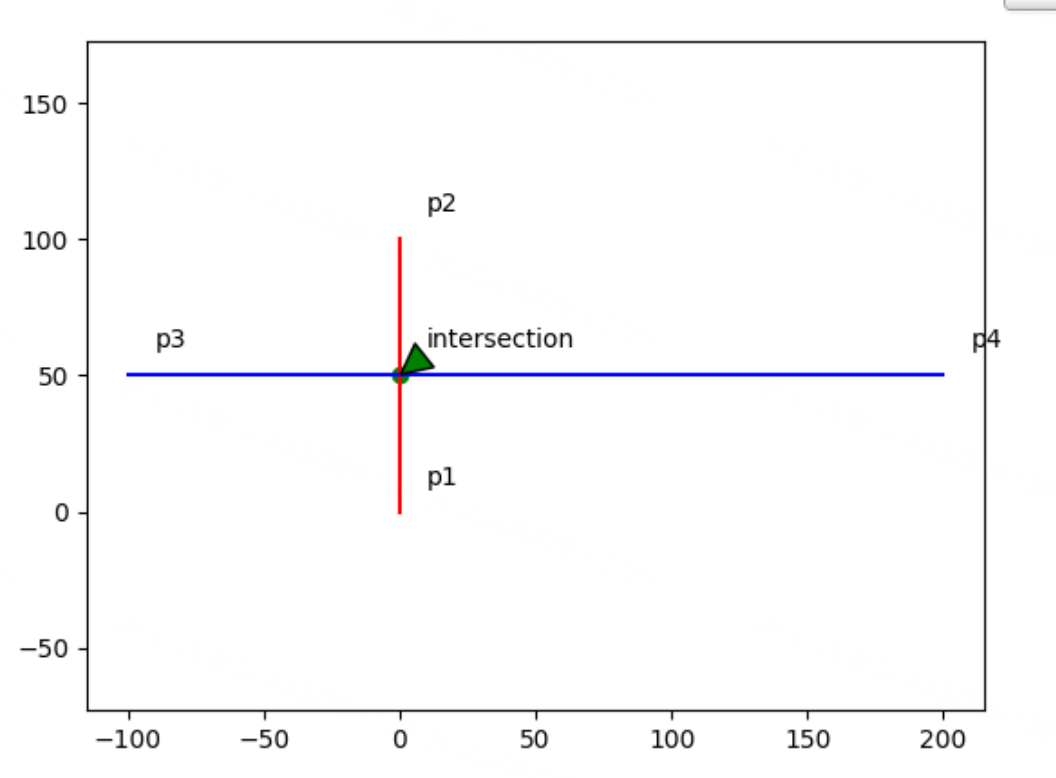
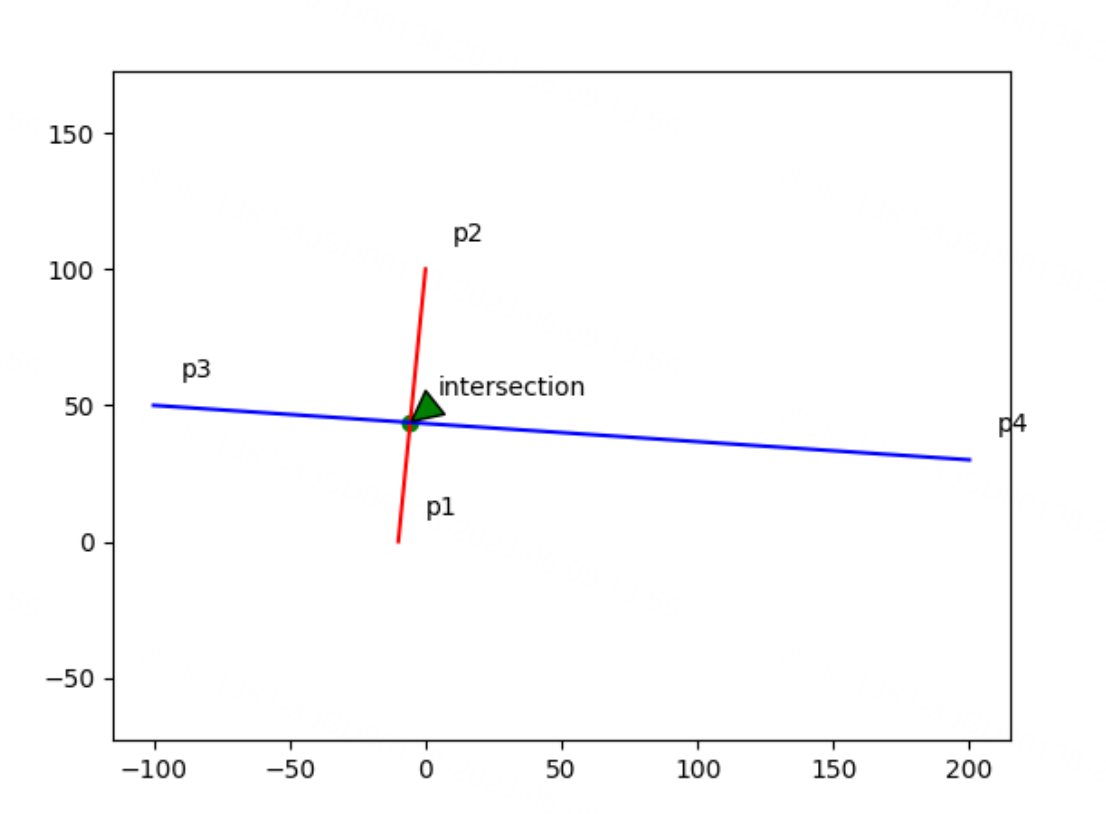
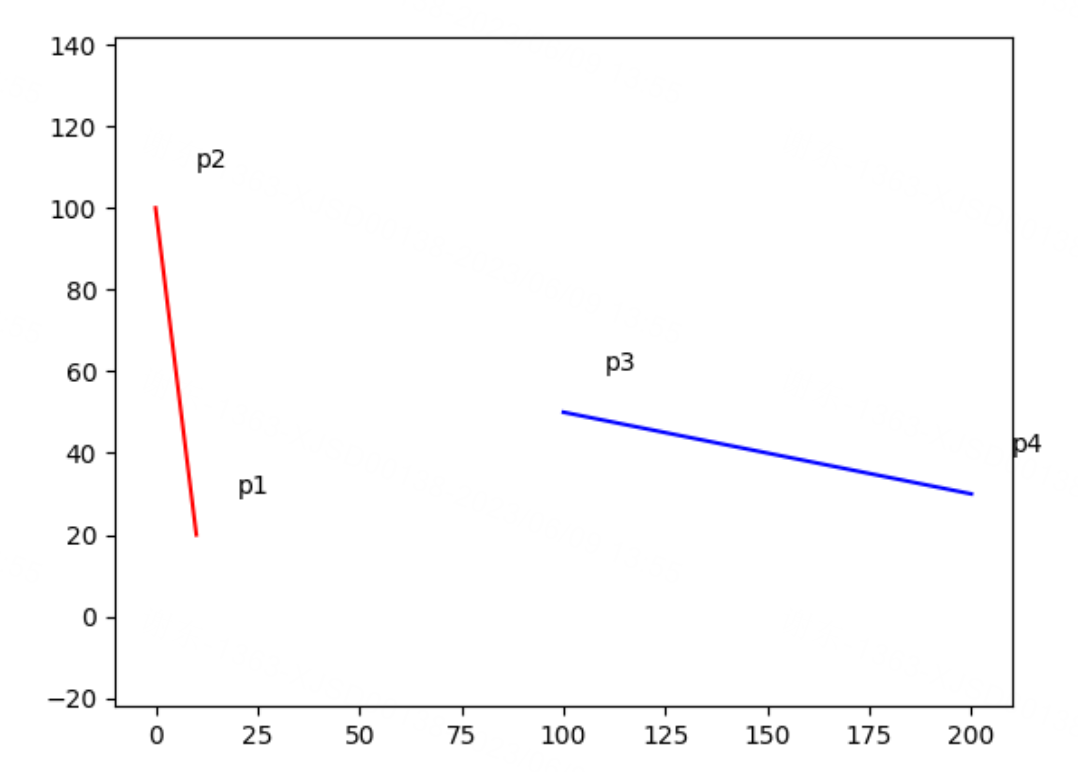
不相交：

C++ 借助opencv的数据结构

cpp
展开代码
float cross(const cv::Point2f& p1, const cv::Point2f& p2, const cv::Point2f& p3) {
    float x1 = p2.x - p1.x;
    float y1 = p2.y - p1.y;
    float x2 = p3.x - p1.x;
    float y2 = p3.y - p1.y;
    return x1 * y2 - x2 * y1;
}
bool has_intersect(const cv::Point2f& p1, const cv::Point2f& p2, const cv::Point2f& p3, const cv::Point2f& p4) {
    // 快速排斥，以l1、l2为对角线的矩形必相交，否则两线段不相交
    if (std::max(p1.x, p2.x) >= std::min(p3.x, p4.x)  // 矩形1最右端大于矩形2最左端
        && std::max(p3.x, p4.x) >= std::min(p1.x, p2.x)  // 矩形2最右端大于矩形最左端
        && std::max(p1.y, p2.y) >= std::min(p3.y, p4.y)  // 矩形1最高端大于矩形最低端
        && std::max(p3.y, p4.y) >= std::min(p1.y, p2.y)) {  // 矩形2最高端大于矩形最低端
        // 若通过快速排斥则进行跨立实验
        if (cross(p1, p2, p3) * cross(p1, p2, p4) <= 0
            && cross(p3, p4, p1) * cross(p3, p4, p2) <= 0) {
            return true;
        }
        else {
            return false;
        }
    }
    else {
        return false;
    }
}
bool has_intersect(const std::vector<cv::Point2f>& seg1, const std::vector<cv::Point2f>& seg2) {
    return has_intersect(seg1[0], seg1[1], seg2[0], seg2[1]);
}
// compute_intersection: 计算两条线段的交点
// 原理：计算两条线段的斜率和截距，然后解方程
cv::Point2f compute_intersection(cv::Point2f p1, cv::Point2f p2, cv::Point2f p3, cv::Point2f p4) {
    cv::Point2f intersection;
    if (p1.x == p2.x) {
        intersection.x = p1.x;
        float slope2 = (p4.y - p3.y) / (p4.x - p3.x);
        float intercept2 = p3.y - slope2 * p3.x;
        intersection.y = slope2 * intersection.x + intercept2;
    } else if (p3.x == p4.x) {
        intersection.x = p3.x;
        float slope1 = (p2.y - p1.y) / (p2.x - p1.x);
        float intercept1 = p1.y - slope1 * p1.x;
        intersection.y = slope1 * intersection.x + intercept1;
    } else {
        float slope1 = (p2.y - p1.y) / (p2.x - p1.x);
        float slope2 = (p4.y - p3.y) / (p4.x - p3.x);
        float intercept1 = p1.y - slope1 * p1.x;
        float intercept2 = p3.y - slope2 * p3.x;
        if (slope1 == slope2) {
            // if p1[0] <= p3[0] <= p2[0]:
            if (p1.x <= p3.x && p3.x <= p2.x) {
                return p3;
            } else if (p1.x <= p4.x && p4.x <= p2.x) {
                return p4;
            } else {
                return {-1, -1};
            }
        }
    }
    return intersection;
}