https://leetcode-cn.com/problems/n-queens/solution/liang-chong-shi-xian-xiang-xi-tu-jie-51-n-huang-ho/

伪代码

python
展开代码
dfs函数(x) { 
    if x==n { //如果x等于n了，说明每行的皇后都放置完毕
        //将棋盘内容的快照保存下来
        return
    }
    for(y=0;i<n;++y) {
        if [x,y]这个位置是有效的，即横、竖、两个斜线都有没有被攻击 {
            将棋盘[x,y]位置设置为 Q
            dfs(x+1) 继续尝试下一行
            将棋盘[x,y]位置还原
        }
    }
}

python3

python
展开代码
class Solution(object):
    def solveNQueens(self, n):
        # 生成N*N的棋盘，填充棋盘，每个格子默认是''.''表示没有放置皇后
        arr = [["." for _ in range(n)] for _ in range(n)]  # 生成列表最好方式是采用列表推导式
        res = []  # 存放最终结果
        # 检查当前的行和列是否可以放置皇后
        def check(x: int, y: int):
            # 检查竖着的一列是否有皇后
            for i in range(x):
                if arr[i][y] == "Q":
                    return False
            # 检查左上的斜边是否有皇后
            i, j = x - 1, y - 1
            while i >= 0 and j >= 0:
                if arr[i][j] == "Q":
                    return False
                i, j = i - 1, j - 1
            # 检查左下的斜边是否有皇后
            i, j = x - 1, y + 1
            while i >= 0 and j < n:
                if arr[i][j] == "Q":
                    return False
                i, j = i - 1, j + 1
            # 检查右上的斜边是否有皇后
            i, j = x + 1, y - 1
            while i < n and j >= 0:
                if arr[i][j] == "Q":
                    return False
                i, j = i + 1, j - 1
            # 检查右下的斜边是否有皇后
            i, j = x + 1, y + 1
            while i < n and j < n:
                if arr[i][j] == "Q":
                    return False
                i, j = i + 1, j + 1
            return True
        def dfs(x):
            # x是从0开始计算的
            # 当x==n时所有行的皇后都放置完毕，此时记录结果
            if x == n:
                res.append(["".join(arr[i]) for i in range(n)])
                return
            # 遍历每一列
            for y in range(n):
                # 检查[x,y]这一坐标是否可以放置皇后
                # 如果满足条件，就放置皇后，并继续检查下一行
                if check(x, y):
                    arr[x][y] = "Q"  # 放上皇后
                    dfs(x + 1)  # 搜索下一行策略
                    arr[x][y] = "."  # 撤销皇后，y进入下一列搜索
        dfs(0)
        return res
print(len(Solution().solveNQueens(8)))

利用一个规律改进算法。之前check()是循环，效率不高。

python3

python
展开代码
class Solution(object):
    def solveNQueens(self, n):
        # 生成N*N的棋盘，填充棋盘，每个格子默认是''.''表示没有放置皇后
        arr = [["." for _ in range(n)] for _ in range(n)]  # 生成列表最好方式是采用列表推导式
        res = []  # 存放最终结果
        columns = set()
        hypotenuse1 = set()
        hypotenuse2 = set()
        # 检查当前的行和列是否可以放置皇后
        def check(x: int, y: int):
            if y in columns:
                return False
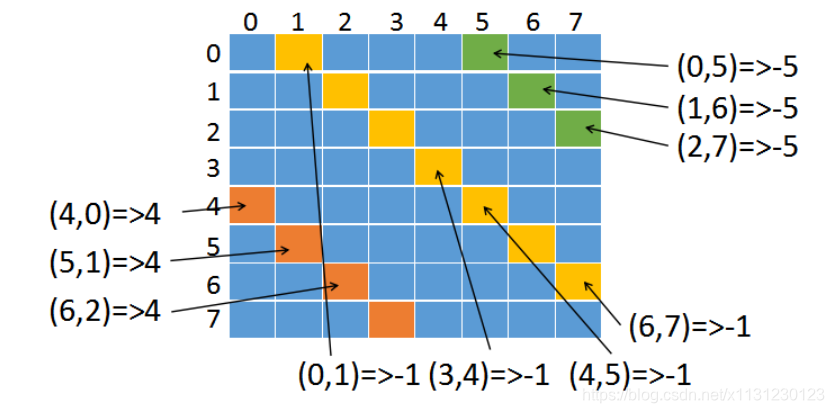
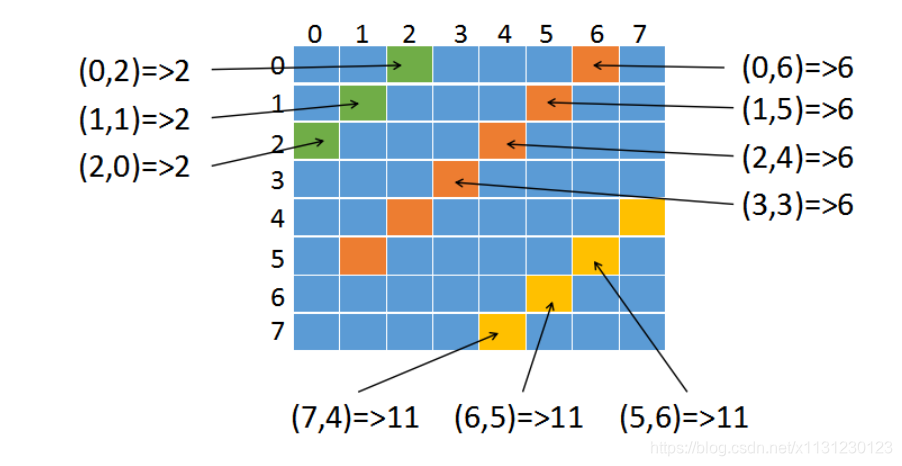
            if x - y in hypotenuse1:
                return False
            if x + y in hypotenuse2:
                return False
            return True
        def dfs(x):
            # x是从0开始计算的
            # 当x==n时所有行的皇后都放置完毕，此时记录结果
            if x == n:
                res.append(["".join(arr[i]) for i in range(n)])
                return
            # 遍历每一列
            for y in range(n):
                # 检查[x,y]这一坐标是否可以放置皇后
                # 如果满足条件，就放置皇后，并继续检查下一行
                if check(x, y):
                    columns.add(y)
                    hypotenuse1.add(x - y)
                    hypotenuse2.add(x + y)
                    arr[x][y] = "Q"  # 放上皇后
                    dfs(x + 1)  # 搜索下一行策略
                    arr[x][y] = "."  # 撤销皇后，y进入下一列搜索
                    columns.remove(y)
                    hypotenuse1.remove(x - y)
                    hypotenuse2.remove(x + y)
        dfs(0)
        return res
print(Solution().solveNQueens(8))